Lineare Gleichungssysteme
Unendlich viele Lösungen
a)
x1 + 3x2 + 2x3 = 2 [1]
2x1 + x2 + 3x3 = 7 [2]
x1 – 2x2 + x3 = 5 [3]
__________________
x 1 + 3x2 + 2x3 = 2 [1]
5x2 + x3 = –3 [4] = [1] – [3]
5x2 + x3 = –3 [5] = 2·[1] – [2]
___________________________
x 1 + 3x2 + 2x3 = 2 [1]
5x2 + x3 = –3 [4]
0 = 0 [6] = [4] – [5]
Der Gleichung [6] entnimmt man, das das LGS unendlich viele Lösungen hat.
Setzt man x2 = t, so folgt x3 = – 3 – 5t; x1 = 8 + 7t.
b)
x1 + x2 – 2x3 = 1 [1]
2x1 + x2 – 3x3 = 2 [2]
_________________
x 1 + x2 – 2x3 = 1 [1]
x2 – x3 = 0 [3] = 2·[1] – [2]
Das LGS hat unendlich viele Lösungen.
Setzt man x3 = t, so folgt x2 = t; x1 = 1 + t.
Wissensteil:
Ein LGS hat keine, genau eine oder unendlich viele Lösungen (vgl. Karte 7).
Unendlich viele Lösungen erkennt man an einer Zeile wie 0 = 0 oder auch 5 = 5. Man wählt dann für eine Variable einen Parameter, z. B. t, und drückt die anderen dann auch durch t aus.
Hinweise zum Gebrauch des GTR beim Lösen eines LGS (vgl. Karte 7)
Zu jedem LGS gehört eine Matrix A. Diese Matrix wird in den GTR eingegeben und mit dem Befehl rref auf die sogenannte reduzierte Stufenform gebracht.
Für die Aufgabe erhält man:
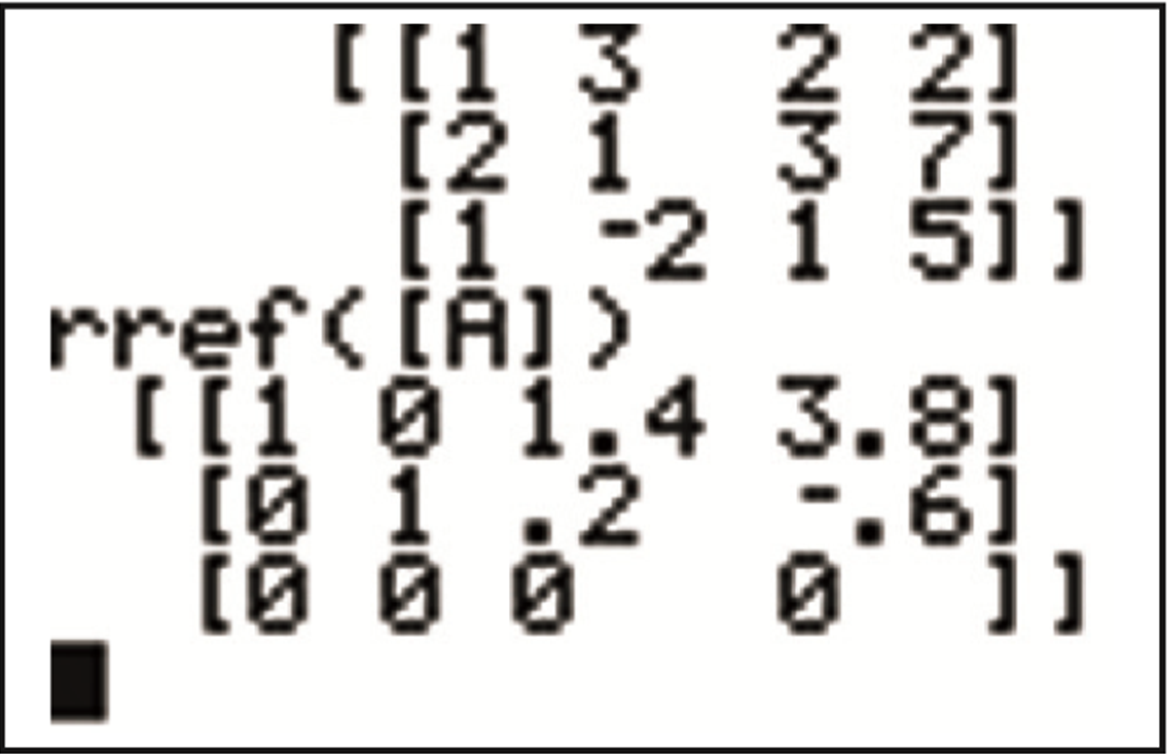
Tipps
Wenn ein LGS unendlich viele Lösungen hat, stellt man die Lösungen mit einem Parameter dar; setzen Sie eine Variable gleich t, so dass wenige Brüche entstehen.
Machen Sie sich klar, was bei einer GTR-Anzeige wie in Fig. die letzte Zeile ausführlich bedeutet: 0·x1 + 0·x2 + 0·x3 = 0.

