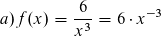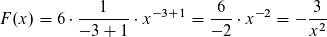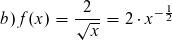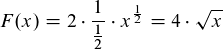Wissensteil:
Integrieren ist das umgekehrte Vorgehen von Differenzieren (Ableiten). Sucht man eine Stammfunktion F zu einer vorgegebenen Grundfunktion f, so ist die Grundfunktion die Ableitung der Stammfunktion. Da konstante Funktionen beim Ableiten null werden, unterscheiden sich zwei Stammfunktionen zur gleichen Grundfunktion um höchstens eine additive Konstante.
Summen- und Faktorregel für Stammfunktionen („Linearität des Integrals“)
Da beim Ableiten die Summen- und Faktorregel gelten (vgl. Karte 29), gelten diese auch beim Bilden einer Stammfunktion (Probe!).
Zusammengesetzte Funktionen werden also stückweise integriert.
Lässt sich f schreiben als
f (x) = c·g (x) + h (x)
und sind F, G und H Stammfunktionen von f, g und h, so gilt
F (x) = c·G (x) + H (x).
Für Potenzfunktionen gilt: Ist f (x) = xz; z ≠ –1, so ist F mit F (x) = 1/z +1 xz+1 eine Stammfunktion von f. Diese Formel gilt auch für rationale Exponenten.
Ergänzung: z = –1:
Da die natürliche Logarithmusfunktion f mit f (x) = ln (x) (x > 0) die Ableitungsfunktion f’ mit
f’ (x) = 1/x besitzt, ist eine Stammfunktion von f (x) = x-1 die Funktion F (x) = ln | x | (x ≠ 0).
Tipps zur Vermeidung von Fehlern
- Schreiben Sie Potenzfunktionen in Bruchschreibweise zunächst mit negativen Hochzahlen, Wurzelfunktionen mit Brüchen als Hochzahlen.
- Berechnen Sie zunächst die neue Hochzahl, dann den neuen Faktor:
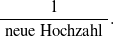
Wandeln Sie nun die Doppelbrüche um.
- Beachten Sie: –3 um 1 erhöht ist –2; – 1/2 um 1 erhöht ist 1/2 .
- Überprüfen Sie Ihr Ergebnis durch Ableiten!
Beispiele: