Home
Niclas König2024-03-14T17:57:32+01:00 BRAINYOO – die mobile
Lehr- und Lernsoftware
- Lernstandserhebungen
- Quiz Battles
- Digitale Prüfungen
- Vokabeltrainer und Karteikarten-App

Kompetenzbasierte Lerninhalte, Lernstandserhebungen, digitale Prüfungen, adaptives selbstgesteuertes Lernen und Gamification in einer Lernsoftware.
Prüfungsvorbereitung und Blended Learning für Ihre Mitarbeiter:innen, Auszubildenden oder Kunden.
Hier gehts zu unserem Online-Shop für digitale Lerninhalte zur individuellen Prüfungsvorbereitung.

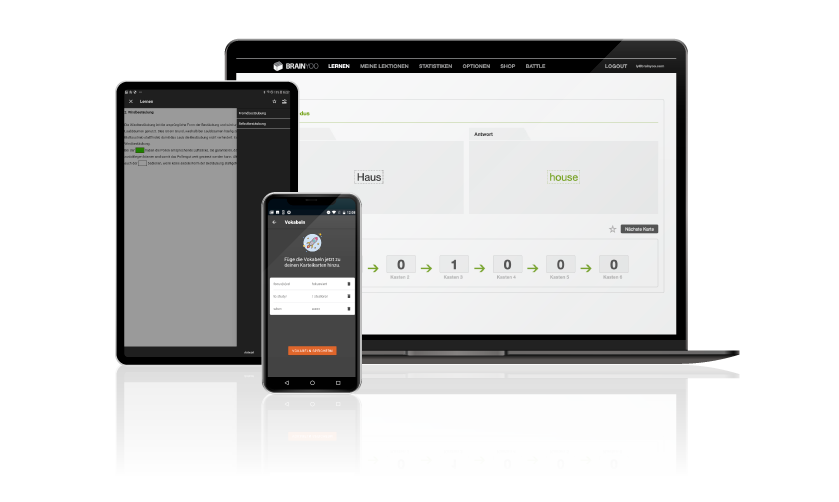
Mobiles Lehren und Lernen
BRAINYOO ist eine mobile Lernplattform und bietet auf Basis von Microlearning-Inhalten eine zeit- und ortsunabhängige Lern- und Lehrunterstützung im Web und via App.
Ob für die Schule, das Studium, die Ausbildung oder eine Weiterbildung gelernt wird: BRAINYOO ist ein didaktischer Werkzeugkoffer für Lehrende zur digitalen Unterrichtsunterstützung und für Lernende eine zielführende Lernbegleitung.
Durch automatische Wiedervorlagen und passenden Lernmodi, kann die Lernsoftware an alle Bedürfnisse angepasst werden.
Zu den klassischen Frage-Antwort-Inhalten gibt es ebenso Lückentext- und Zuordnungsaufgaben, Vokabelkarten sowie die Möglichkeit Aufgaben im Multiple-Choice-Format zu erstellen.
Die insbesondere auf Tablet & Co. ausgerichtete mobile App stellt durch die Kamera-, Audio- und Scan-and Translate-Funktion einen echten Mehrwert dar, um Inhalte multimedial anzureichern und fremdsprachliche Inhalte direkt zu generieren:
Mit dem integrierten PONS Wörterbuch in acht Fremdsprachen sowie der Scan-and-Translate-Funktion können fremdsprachliche Texte eingescannt sowie unbekannte Vokabeln direkt übersetzt und bei Bedarf als Vokabel-Lernkarten angelegt werden.
Scanne alternativ eine Vokabelliste ein und konvertiere diese in Vokabelkarten, um sie dann mit BRAINYOO zu lernen.
Weitere Funktionen wie digitale Prüfungen mit automatischer Bewertung, individuelle Lernstatistiken, Quiz-Battles und Lernerinnerungen runden das digitale Lehren und Lernen ab!
Motivierende
Quiz-Battles
Homo ludens – Der Mensch entwickelt seine Fähigkeiten im Spiel. Das Battle ist eine spielerische Lernaktivität, die ganze Klasse tritt live gegeneinander an und beantwortet an mobilen Endgeräten oder am PC Fragen.
Zeitsparende Lernstandserhebungen
Die individuellen Lernstände können innerhalb von Lerngruppen von allen Lerngruppen-mitgliedern abgerufen werden. Die Lernfortschritte werden mit Hilfe aussagekräftiger Grafiken visualisiert.
Digitale Prüfungen / automatisierte Bewertungen
Aus bestehenden Inhalten können digitale Lernkontrollen angelegt und für die Bearbeitung ein Zeitlimit gesetzt werden. Die Bewertung geschieht automatisch und lässt sich bei Bedarf zustätzlich manuell bearbeiten.
Selbstgesteuertes
Lernen
Der lernoptimierte Algorithmus berücksichtigt individuelle Lernergebnisse und strukturiert das Lernen durch eine automatische Wiedervorlage mit Lernzeit-Erinnerung durch Push-Nachrichten. So ergeben sich individuelle Lernpfade.
Überall lernen
SIE HABEN FRAGEN ZU BRAINYOO?
Rufen Sie uns an unter
Schreiben Sie uns unter
Expertenmeinungen
Mit Hilfe von BRAINYOO können Schüler:innen individuell arbeiten, ich habe dabei jederzeit einen Überblick über ihren aktuellen Lernstand. Diesen kann ich für meine Unterrichtsplanung berücksichtigen und so die Förderung der Schüler:innen verbessern.
Unsere Partner